4 Ways To Find Height of A Binary Tree In Java | Java Programming

Java code to calculate the height of a binary tree – In this article, we will be discussing the various ways to calculate the height of a binary tree in Java programming.

Suitable examples and sample programs have been included in order to make you understand simply. The compiler has also been added so that you can execute the programs yourself.

The methods that have been used in this article are as follows:

• Using Standard Method
• Using Scanner Class
• Using Static Method
• Using Separate Class
• Using Command Line Arguments

A binary tree is a tree-type data structure which is predominantly used. It has two tree nodes or children. Those are named as:

• Left Child
• Right Child

Usually, the left child has a smaller value than the parent and the right child has a greater value than the parent.

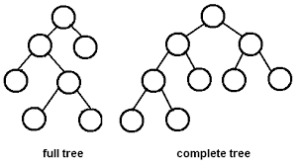
As you can see in the image above, there are two specific types of binary trees:

• Full Tree
• Complete Free

Using Standard Method

The input required for this is the number of nodes so, we give this input in the code itself and assign it to a variable (nodes). Here as we are talking about binary tree, every node has 2 child nodes at the same level or height.

So to find the length of the node, to avoid counting the nodes in the same level we keep dividing the number of nodes by 2 at each level and increment the height count (c) by one. This is done until we are left with only a single node with is at level 0. This is done with the help of an iterative while loop as follows:

This final value of the height count variable (c) is the height of the binary tree. But, let us consider the worst case where, every node has only a single child node. Under this case, our worst case possible height of the node is initial number of nodes-1.

This is why before performing the iteration of variable nodes we store it in another variable (n) so that, it can be used to calculate the worst case height i.e., n-1.

Output:

Using Scanner Class to Find Height of A Binary Tree

In the above method, we have seen that, the number of nodes is already given in the code and to try the code for a different output, the change must be made in the code itself. To avoid this circumstance, we make use of Scanner class in Java to read any primitive input at runtime by giving value in the console screen.

Here, we read the number of nodes (nodes) with the use of scanner class and following which the same logic and set of statements used above is made use of here also to determine the height of the binary tree.

Output1:

Using a Static Method

This method is implemented in order to make the code reusable. Above, we can observe that entire code is within main method and if the statements are to be made use of at later part of the code, they have to be rewritten.

Instead, we can place the main logic of calculating the height of binary tree as discussed earlier is placed within a separate static method (binaryTreeCal) and the main method reads input number of nodes (nodes) using Scanner class and passes this as an argument while calling the other static method (binaryTreeCal).

This method returns an integer value after calculation which denotes the height of the binary tree which is our resultant output.

Output1:

 

Using Separate Class

We can split the code into parts based on logic and place it in separate class to increase the readability of the code.Here, a separate class (HeightCal) is created which contains the earlier discussed logic to determine the height of the binary tree in the constructor of the class (HeightCal).

The resultant value is also stored in the variable (c) of the same class (HeightCal).

In the class with main method (BT), the main method reads the input number of nodes (nodes) using Scanner class. An object (h) is created in the main method which references the other separate class (HeightCal) and passes input as parameter.

With creation of object the constructor is invoked and the height of the binary tree is determined and stored in the variable (c). This variable is invoked with the created object (h) and displayed in the console screen as height of the binary tree and at worst case the height is number of nodes-1.

Output1:

Using Command-Line Arguments

Instead of using the Scanner class, we can also pass input at runtime by command-line arguments. While writing the run command, a single argument (args[0]) can be sent with a space in between to the code. This argument which is in string format can be converted to integer format by parsing as follows:

This parsed and converted value is then stored in a variable (nodes) representing the number of nodes in a binary tree which is our input. After getting the input, the same steps as discussed in the beginning are followed to determine the height of the binary tree.

Output: