C Constants – Tutorial With Examples | C Programming

From the list of C tutorials, another guide for c learners on C constants. C constants with example programs and syntax. Do check it out.

• What are C constants?

Constants in any language would depend on the types of data the language supports.

Basically C language has 4 data types and obviously we can say that there are 4 types of constants.

• The data types “char”, “int”, “float” and “double” represent different types of constants we have.

Out of them “float” and “double” represent the numbers with decimal points (Eg: 3.4, 56.33). “int” represents the whole numbers (Eg: 24, 4322). “char” represent the ASCII characters (Eg: ‘A’, ‘e’, ‘5’, ‘+’).

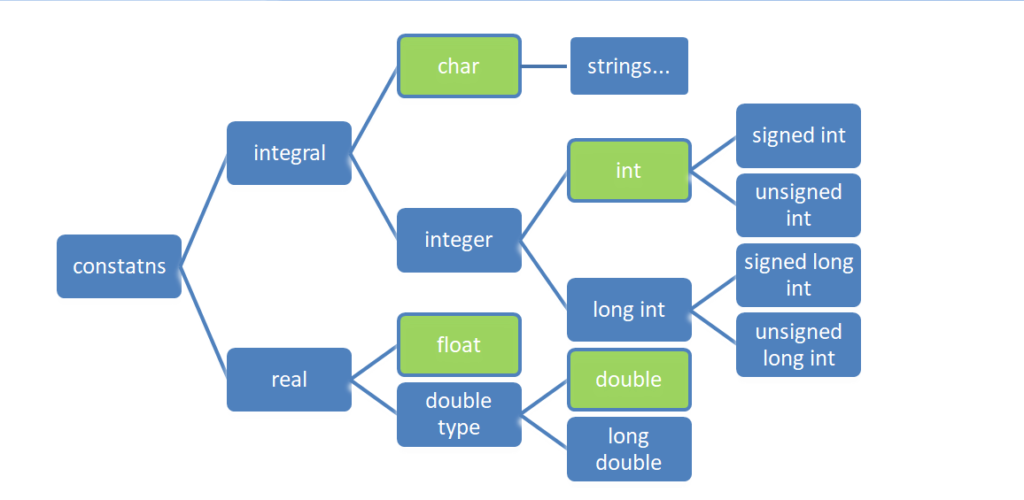
• Basically constants are divided into 2 types i.e. integral and real.
• The integral types are divided into ‘char’ and integer types.
• The ‘char’ type can be used to store any of the 256 ASCII characters (numbered from 0 to 255).
• A set of characters (terminated by a null character) is known as a string.
• To store integer type data, we use two types ‘int’ and ‘long int’.
• The ‘long int’ can store bigger range of values compared to normal ‘int’.
• When we are working with all positive numbers, we can use ‘unsigned int’, and for bigger numbers we can use ‘unsigned long int’.
• By default, ‘int’ means ‘signed int’ where as ‘long int’ means ‘signed long int’.
• The ‘float’, ‘double’ and ‘long double’ types are used to store numbers with decimal points.
• The ‘double’ can hold bigger values compared to ‘float’ and ‘long double’ can hold bigger values compared to ‘double’.
• The ‘double’ type can give better accuracy compared to ‘float’ type.

What are Character Constants?

We have 256 character constants in C language and they are from ASCII set. To store any such character, a C compiler takes 1 byte of memory (8 bits).

Each character is numbered so that that number would be stored inside the system when we try to store the corresponding character.

Suppose, for the character ‘A’, the assigned number is 65 and binary value of 65 (01000001) is actually stored inside the system when we try to store ‘A’.

similarly when we want to store the newline character (‘\n’) in the system, its binary value 01001010 (ASCII value 10) is actually stored.

In the following table, we can see some of the regularly used characters, their ASCII value (ASCII code) and the binary representation.

Regular Used Characters:

General name	ASCII Character/Symbol	ASCII code	Binary value
Null character	‘\0’	0	00000000
	☺	1	00000001
	☻	2	00000010
	♥	3	00000011
	♦	4	00000100
	♣	5	00000101
	♠	6	00000110
Alert bell (beep sound)	‘\a’	7	00000111
Backspace (cursor one step behind in the current line)	‘\b’	8	00001000
Tab	‘\t’	9	00001001
Newline (cursor to beginning of the next line)	‘\n’	10	00001010
(Vertical tab) ‘\v’	♂	11	00001011
(form feed) ‘\f’	♀	12	00001100
Carriage return (cursor to beginning of same line)	‘\r’	13	00001101
	♫	14	00001110
	☼	15	00001111
	►	16	00010000
	◄	17	00010001
	↕	18	00010010
	‼	19	00010011
	¶	20	00010100
	§	21	00010101
	▬	22	00010110
		23	00010111
	↑	24	00011000
	↓	25	00011001
	→	26	00011010
	←	27	00011011
	∟	28	00011100
	↔	29	00011101
	▲	30	00011110
	▼	31	00011111
Space		32	00100000
Exclamation	!	33	00100001
		34	00100010
Hash	#	35	00100011
Dollar	$	36	00100100
Percentile	%	37	00100101
Ampersand (and)	&	38	00100110
Single quote	‘	39	00100111
Left parentheses	(	40	00101000
Right parentheses	)	41	00101001
Asterisk (star)	*	42	00101010
Plus	+	43	00101011
Comma	,	44	00101100
Minus (hyphen)	–	45	00101101
Dot	.	46	00101110
Forward slash	/	47	00101111
Digits start here…
Character 0	0	48	00110000
	1	49	00110001
	2	50	00110010
Character 3	3	51	00110011
	4	52	00110100
	5	53	00110101
	6	54	00110110
	7	55	00110111
	8	56	00111000
Character 9	9	57	00111001
Colon	:	58	00111010
Semi-colon	;	59	00111011
Less than	<	60	00111100
Equals / assignment	=	61	00111101
Greater than	>	62	00111110
Question mark	?	63	00111111
At the rate	@	64	01000000
Upper case alphabets start here…
	A	65	01000001
	B	66	01000010
	C	67	01000011
	D	68	01000100
	E	69	01000101
	F	70	01000110
	G	71	01000111
	H	72	01001000
	I	73	01001001
	J	74	01001010
	K	75	01001011
	L	76	01001100
	M	77	01001101
	N	78	01001110
	O	79	01001111
	P	80	01010000
	Q	81	01010001
	R	82	01010010
	S	83	01010011
	T	84	01010100
	U	85	01010101
	V	86	01010110
	W	87	01010111
	X	88	01011000
	Y	89	01011001
	Z	90	01011010
Left bracket	[	91	01011011
Back slash	\	92	01011100
Right bracket	]	93	01011101
Cap / carrot	^	94	01011110
Underscore	_	95	01011111
	`	96	01100000
Lower case alphabets start here…
	a	97	01100001
	b	98	01100010
	c	99	01100011
	d	100	01100100
	e	101	01100101
	f	102	01100110
	G	103	01100111
	h	104	01101000
	i	105	01101001
	j	106	01101010
	K	107	01101011
	l	108	01101100
	m	109	01101101
	n	110	01101110
	o	111	01101111
	p	112	01110000
	q	113	01110001
	r	114	01110010
	s	115	01110011
	t	116	01110100
	u	117	01110101
	v	118	01110110
	w	119	01110111
	x	120	01111000
	y	121	01111001
	z	122	01111010
	{	123	01111011
	|	124	01111100
	}	125	01111101
	~	126	01111110
	⌂	127	01111111

 

What are Integer Constants?

Any whole number (which does not contain a decimal point) is an integer. An integer can be a positive number or a negative number.

• Eg1:        13
• Eg2:        5999
• Eg3:        -552

Generally integers are represented in decimal number system. The above 3 values (13, 5999 and -552) are in decimal number system format only.

If we want, we can represent the numbers in octal number system and hexa-decimal number system also.

An octal number is identified by a normal number preceded by 0 (zero) and a hexa decimal number is identified by a normal number preceded by 0x (zero x).

• 25           is decimal number
•  025         is octal number (which is equivalent to decimal 21)
• 0x25       is hexa decimal number (which is equivalent to decimal 37)

Decimal	octal	hexa decimal
0	00	0x0
1	01	0x1
2	02	0x2
3	03	0x3
4	04	0x4
5	05	0x5
6	06	0x6
7	07	0x7
8	010	0x8
9	011	0x9
10	012	0xa
11	013	0xb
12	014	0xc
13	015	0xd
14	016	0xe
15	017	0xf
16	020	0x10
17	021	0x11
18	022	0x12
19	023	0x13
20	024	0x14
21	025	0x15
22	026	0x16
23	027	0x17
24	030	0x18
25	031	0x19
26	032	0x1a
27	033	0x1b
28	034	0x1c
29	035	0x1d
30	036	0x1e
31	037	0x1f
32	040	0x20
33	041	0x21
34	042	0x22
35	043	0x23
36	044	0x24
37	045	0x25
38	046	0x26
39	047	0x27
40	050	0x28

The long int are good to store bigger values compared to normal int type. Generally the long int type numbers are suffixed with an ‘l’ or ‘L’.

Eg1:        long int a=34L;

Eg2:        long int a=34l;

Eg3:        long int a=34;

Eg4:        long int a=12345678L;

The float and double constants :-

The numbers with decimal points (with fractional parts) are represented using ‘float’ and ‘double’ types.

The double is better in terms of accuracy and can hold bigger values compared to ‘float’.

These values are represented in two forms i.e. fixed and exponential.

• Eg1:        3456.3                   is fixed format
• Eg2:        3.4563e3              is exponential format

The exponential format is very much useful when working with very large numbers or very small numbers.

To represent a number 123000000000000.0, we can write it as 1.23*10¹⁴ mathematically. But we cannot write the superscript and subscript type of things in a program. So the 1.23*10¹⁴ is written in a program as 1.23e14 and the number 0.000000000023 can be written as 2.3e-11 (which is written as 2.3*10^-11 mathematically).

We can store 4.5 as a ‘float’ value, as a ‘double’ value and also as a ‘long double’ value.

• Eg1:        float a=4.5;
• Eg2:        double a=4.5;
• Eg3:        long double a=4.5;

To differentiate between them some compilers accept the following notations.

• Eg1:        float a=4.5F;
• Eg2:        double a=4.5;
• Eg3:        long double a=4.5L;

A real number suffixed with an ‘f’ or ‘F’ is treated as ‘float’ and when suffixed with ‘l’ or ‘L’ is treated as ‘long double’. By default, a real number is treated as a ‘double’ type.