Learn Java Java Tutoring is a resource blog on java focused mostly on beginners to learn Java in the simplest way without much effort you can access unlimited programs, interview questions, examples
Java Program To Calculate Log() – In this article, we will brief in on all the possible ways to log in Java. Log Java code has been written in all possible ways here. If you have any queries leave a comment here.
The methods used in this article are as follows:
- Using Standard Class
- Using Scanner Class
- Using Predefined Method
- Using Static Method
- Using Separate Class
Logarithm, as we all know, is the inverse function to the exponentiation. A logarithm of a number given is equal to the exponent to which another number, the base is raised to the power of.
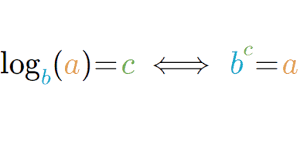
As you can see in the image, the quantity in the left-hand side is referred to as log a to the base “b” or simply log a.
The base part is excluded when the value generally is 10 or e.
Logarithms with base 10 are represented as log, which is known as Common Logarithms. Similarly, logarithms with base e are represented as ln, known as Natural Logarithms.
Thus, the multiple ways to calculate log in Java Programming are as follows:
Log() Java – Standard Method
The standard approach to solving this problem is to first take input in the code itself. The input for our given problem is an integer number.
To find log in java, to make things simpler, the Math package in Java already has a built in method named log for this.
If you need log for base 10 you can use the Math.log10() for base e, it is Math.log().
These methods are already predefined so, to get the desired output you just need to directly call this function and display in the output screen.
|
1 2 3 4 5 6 7 8 9 10 11 |
class Log { public static void main(String arg[]) { int n=10; System.out.println("n= "+n); System.out.println("Common logarithm value of n is "+(Math.log10(n))); System.out.println("Natural logarithm of " + n + " = " + Math.log(n)); } } |
Output:
|
1 2 3 |
n= 10 Common logarithm value of n is 1.0 Natural logarithm of 10 = 2.302585092994046 |
Using Scanner Class
Instead of giving input in the code, using Scanner class in Java, we can read input at runtime itself. So, making use of this for our problem, we read the inputs – number whose log has to be found (n) and the base for log (b).
As log is not fixed,it could be anything other than 10 or e. Under such a scenario the built in methods for log can’t be used.
So, the logic here is that, we take another variable (c). Until the number n remains greater than 1, we keep dividing the number (n) with the base (b) and increment variable (c) by 1 every time.
|
1 2 3 |
while(n>1) { n=n/b; c++; } |
After coming out of this iterative loop, we add the number (n) after iteration to the variable (c).
Our output for log n base b is approximately now equal to (c-1). Just to give you clarity, the output value here is only the approximate value and not the exact value.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 |
import java.util.Scanner; class Log { public static void main(String arg[]) { Scanner sc=new Scanner(System.in); System.out.println("enter a number n :"); double n=sc.nextDouble(); System.out.println("enter a base number "); double b=sc.nextDouble(); double c=0; while(n>1) { n=n/b; c++; } c=c+n; System.out.println("log value of n approximately equals to: "+(c-1)); } } |
Output:
|
1 2 3 4 5 |
enter a number n : 10 enter a base number 10 log value of n approximately equals to: 1.0 |
Log Java – Using Predefined Method
As we have seen in the first method of this problem, there are predefined methods in Math package to find the log of a number given that its base is either 10 or e.
For base 10, it is Math.log10() whereas for base e, it is Math.log() method.
But, in the standard method, we took the input in the code itself which is not an efficient way for writing a code.
This is because, if it is written in the code itself then, for every testcase, we must go and make changes in the code. So instead, we make use of the Scanner class that is discussed above to read the input number at runtime.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 |
import java.util.Scanner; class Log { public static void main(String arg[]) { Scanner sc=new Scanner(System.in); System.out.println("enter a number "); double n=sc.nextDouble(); System.out.println("Common logarithm value of n is "+(Math.log10(n))); System.out.println("Natural logarithm of " + n + " = " + Math.log(n)); } } |
Output:
|
1 2 3 4 |
enter a number 10 common logarithm value of n is 1.0 Natural logarithm of 10.0 = 2.302585092994046 |
Using Static Method
This method is being made use of in order to increase the readability of the code as well as to make the logic reusable.
The logic remains the same here, we read the two inputs- the number and the base.
Then the method discussed under the scanner class is made use of. The resultant value is the subtracted by 1 same as above which is the log of the number for the given base.
The difference here is that, the code it split into parts.
The input output operations are taken care of by the main method while the logic for calculating the log is taken care of by another static method (logCal) by passing the input values as its arguments.
The linking between these two is that, in the main method, the other static method (logCal) is called which returns our desired value.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 |
import java.util.Scanner; class Log { public static void main(String arg[]) { Scanner sc=new Scanner(System.in); System.out.println("enter a number n :"); double x=sc.nextDouble(); System.out.println("enter a base number "); double y=sc.nextDouble(); double res=logCal(x,y); System.out.println("log value of n approximately equals to: "+(res-1)); } static double logCal( double n, double b) { double c=0; while(n>1) { n=n/b; c++; } c=c+n; return c; } } |
Output:
|
1 2 3 4 5 |
enter a number n : 27 enter a base number 3 log value of n approximately equals to: 3.0 |
