Learn Java Java Tutoring is a resource blog on java focused mostly on beginners to learn Java in the simplest way without much effort you can access unlimited programs, interview questions, examples
Java code To Calculate Median – In this article, we will brief in on the mentioned means to Finding the middle element in array. The following median code has been written in 4 different ways. If you have any doubts you can leave a comment here.
The source code has written in:
- Using Standard Method
- Using Static Method
- Using Scanner Class
- Using Command Line Arguments
- Using Separate Class
The median of a given group of data is the value which falls in between of the given values. The only difference between Median and Mean is that Mean gives a rough average of the whole data.
Whereas the median will give the exact value which falls in between of the smallest and highest values.
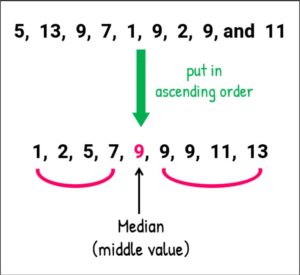
As you can see, in the given order of values, firstly, it has to be arranged in an ascending or descending order. Then, the middle value is noted down.
9 is the middle value of the given set of numbers. Thus, 9 is the median of the group.
Calculate Median Array – Standard Method
For this problem, we first taken the inputs. The inputs are the number of elements or the size of array and the data values which are to be stored in the array (a).
One important thing to be kept in mind is that the data values are to be entered in a sorted order. This is necessary because we need to find the middle element.
After taking the inputs, we need to first check whether the number of elements is odd or even.
- if(n%2==1)
- If the number of elements is odd then, the center-most element is the median.
- m=a[(n+1)/2-1];
- Else, the average of the two middle elements.
- m=(a[n/2-1]+a[n/2])/2;
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 |
class Median { public static void main(String arg[]) { int n=5; double a[]=new double[n]; a[0]=10; a[1]=20; a[2]=30; a[3]=40; a[4]=50; double m=0; if(n%2==1) { m=a[(n+1)/2-1]; } else { m=(a[n/2-1]+a[n/2])/2; } System.out.println("Median :"+m); } } |
Output:
|
1 |
Median :30.0 |
Using Static Method
In the case of making use of static method, we split up the code into two parts.
The inputs i.e., the size of array and data values of array in a sorted order, is read using the scanner class.
After reading the inputs, another static method is called to which the inputs are passed as arguments.
This method consists of set of statements to return the mean based on the same logic as discussed above. T
In this, both the main method as well as the static method are written within the same class.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 |
import java.util.Scanner; class Median { public static void main(String args[]) { Scanner sc=new Scanner(System.in); System.out.println("enter a number"); int a=sc.nextInt(); double[] input=new double[a]; System.out.println("enter "+a+" elements"); for(int i=0;i<a;i++) { input[i]=sc.nextDouble(); } double res=medianCal(a,input); System.out.println("Median :"+res); } static double medianCal(int n,double in[]) { double m=0; if(n%2==1) { m=in[((n+1)/2)-1]; } else { m=(in[n/2-1]+in[n/2])/2; } return m; } } |
Output1:
|
1 2 3 4 5 6 7 8 |
enter a number 4 enter 4 elements 1 2 3 4 Median :2.5 |
Using Scanner Class
In the above example, we had mentioned that, the inputs are taken making use of the scanner class.
Scanner class in Java is that class which reads input at runtime given by the tester/user for any primitive datatype.
So here, we make use of the scanner class to first read an integer number which is considered as the size of array (total number of data values) followed by which we take the data values which could either be integers or decimal value and therefore, we choose double type. It is essential to make sure that, these data values must be taken in sorted order only.
After gathering the inputs, we will find the median of the given data values with the same logic as explained above.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 |
import java.util.Scanner; class Median { public static void main(String args[]) { Scanner sc=new Scanner(System.in); System.out.println("enter a number"); int n=sc.nextInt(); double[] input=new double[n]; System.out.println("enter "+n+" elements"); double m=0; for(int i=0;i<n;i++) { input[i]=sc.nextDouble(); } if(n%2==1) { m=input[(n+1)/2-1]; } else { m=(input[n/2-1]+input[n/2])/2; } System.out.println("Median :"+m); } } |
Output:
|
1 2 3 4 5 6 7 8 9 |
enter a number 5 enter 5 elements 1 2 3 4 5 Median :3.0 |
Using Command Line Arguments
Apart from making use of scanner class to take inputs at runtime, we can also give values along with the run command itself separated by space between each argument.
This method is called the using of command line arguments.
Here, we first give the number of elements (arg[0]) followed by which we give as many arguments having data values as mentioned. These variables are first converted to their respective datatypes using parsing and then stored in the variable.
After acquiring all the inputs the same steps as mentioned in the beginning are followed.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 |
class Median { public static void main(String args[]) { int n=Integer.parseInt(args[0]); double[] input=new double[n]; double m=0; for(int i=0;i<n;i++) { input[i]=Double.parseDouble(args[i+1]); } if(n%2==1) { m=input[(n+1)/2-1]; } else { m=(input[n/2-1]+input[n/2])/2; } System.out.println("Median :"+m); } } |
Using Separate Class
To enhance the readability and make things smoother to find any part of the code if we ever require to make modifications in the future, we split the code into different classes.
Here, the class containing main method has all the necessary input operations using the scanner class. This is followed by creating of an object referencing another class (MedianCal).
This separate class (MedianCal) has a constructor which is responsible for performing set of instructions as mentioned above to find the median and store it in a variable of the separate class (MedianCal).
This variable is called in the main method with the help of the object created and printed as output.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 |
import java.util.Scanner; class MedianCal { double m=0; MedianCal(int n,double in[]) { if(n%2==1) { m=in[((n+1)/2)-1]; } else { m=(in[n/2-1]+in[n/2])/2; } } } class Median { public static void main(String args[]) { Scanner sc=new Scanner(System.in); System.out.println("enter a number"); int a=sc.nextInt(); double[] input=new double[a]; System.out.println("enter "+a+" elements"); for(int i=0;i<a;i++) { input[i]=sc.nextDouble(); } MedianCal res=new MedianCal(a,input); System.out.println("Median :"+res.m); } } |
Output:
|
1 2 3 4 5 6 7 8 9 |
enter a number 5 enter 5 elements 1 2.5 3 3.5 4 Median :3.0 |
