Learn Java Java Tutoring is a resource blog on java focused mostly on beginners to learn Java in the simplest way without much effort you can access unlimited programs, interview questions, examples
Java program to find out the GCD between two numbers. Here, we will discuss the various methods to find out the GCD between two numbers. Also, we’ll learn how to calculate the GCD of n numbers. Soon Compiler has added to it so that you can execute the set of programs yourself. The methods as aforementioned are:
- Using Static Method
- Using While Loop
- Using Functions
- Using Recursion
GCD or Greatest Common Divisor of two or more given numbers is the largest value that divides the given numbers wholly, without leaving any fraction behind.
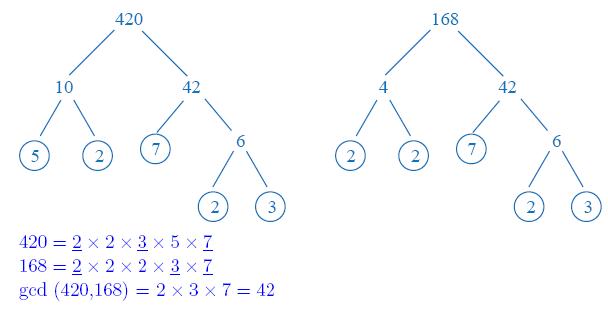
As in the example shown below, we take two numbers 420 and 168.
After Prime Factorization, we get that
168 = 2 * 2 * 2 * 3 * 7
420 = 2 * 2 * 3 * 5 * 7
The common factors are 2 * 3 * 7 = 42.
Hence, the GCD of 168 and 420 is 42.
Using Static Method
1) Read the values using scanner class method sc.nextInt(),and store those values in to the variables n1,n2.
If both the numbers n1,n2>0 then call the static method gcdCal(n1,n2) in main method.
2) The n1,n2 values will be passed to a,b and Checks the while condition b>0,if the condition is true then b assigned to temp, b=remainder of b/a, “a” initialized with temp, repeats until the while condition b>0 is false and returns the “a” value which is GCD of two numbers.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 |
import java.util.Scanner; class Gcd { public static void main(String arg[]) { long n1,n2; Scanner sc=new Scanner(System.in); System.out.println("enter number 1"); n1=sc.nextLong(); System.out.println("enter number 2"); n2=sc.nextLong(); if(n1>0 && n2>0) { long result=gcdCal(n1,n2); System.out.println("Gcd of two numbers = "+result); } else System.out.println("Please enter numbers greater than zero"); } static long gcdCal(long a,long b) { while (b > 0) { long temp = b; b = a % b; a = temp; } return a; } } |
Output:
|
1 2 3 4 5 |
enter number 1 25 enter number 2 50 Gcd of two numbers = 25 |
Using While Loop
1) Read the values using scanner class object and assign those values to the variables x,y.
2) If both the numbers greater than 0, then checks the while condition while(x!=y), if it is true – then if x>y then x=x-y else y=y-x.
3) Repeat until x!=y and returns the x value which is the GCD of two numbers.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 |
import java.util.Scanner; class Gcd { public static void main(String arg[]) { long x,y; Scanner sc=new Scanner(System.in); System.out.println("enter number 1"); x=sc.nextLong(); System.out.println("enter number 2"); y=sc.nextLong(); if(n1>0 && n2>0) { while(x!=y) { if(x>y) x=x-y; else y=y-x; } System.out.println("Gcd of two numbers is="+x); } else System.out.println("Please enter numbers greater than zero"); } } |
Output:
|
1 2 3 4 5 |
enter number 1 24 enter number 2 48 Gcd of two numbers is=24 |
Using Functions
1) In this program we have a function long greater(long a, long b), it calculates the GCD of two numbers a,b and returns the number.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 |
import java.util.Scanner; class GcdCalculation { long greater(long a,long b) { while(a!=b) { if(a>b) a=a-b; else b=b-a; } return a; } } class Gcd { public static void main(String arg[]) { GcdCalculation g=new GcdCalculation( ); long n1,n2; Scanner sc=new Scanner(System.in); System.out.println("Enter first number"); n1=sc.nextLong(); System.out.println("Enter second number"); n2=sc.nextLong(); if(n1>0 && n2>0) System.out.println("Gcd of two numbers is="+g.greater(n1,n2)); else System.out.println("Values should be greater than 0 otherwise gcd is 0"); } } |
Output:
|
1 2 3 4 5 |
Enter first number 5 Enter second number 10 Gcd of two numbers is=5 |
Using Recursion
1) In this program greater(long a, long b) calls itself as greater(a,b), the greater method is a recursive method. It repeats until if the condition is false and returns “a” value which is GCD of a,b.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 |
import java.util.Scanner; class GcdCalculation { long greater(long a,long b) { if(a!=b) { if(a>b) a=a-b; else b=b-a; return greater(a,b); } return a; } } class Gcd { public static void main(String arg[]) { GcdCalculation g=new GcdCalculation( ); long n1,n2; Scanner sc=new Scanner(System.in); System.out.println("Enter first number"); n1=sc.nextLong(); System.out.println("Enter second number"); n2=sc.nextLong(); System.out.println("Gcd of two numbers is="+g.greater(n1,n2)); } } |
Output:
|
1 2 3 4 5 |
Enter first number 25 Enter second number 3 Gcd of two numbers is=1 |
Finding GCD for n numbers
1) To store elements into the int array
2) Find GCD of n numbers by passing “r” value and each element of an array to the constructor as GcdCalculation(long a, long b).
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 |
import java.util.Scanner; class GcdCalculation { long r; GcdCalculation(long a,long b) { while (b > 0) { long temp = b; b = a % b; a = temp; r=a; } } } class Gcd { public static void main(String arg[]) { { GcdCalculation result; Scanner sc=new Scanner(System.in); System.out.println("Enter how many numbers you want"); int n=sc.nextInt(); long input[]=new long[n]; System.out.println("Enter "+n+" numbers"); for(int i=0;i<n;i++) { input[i]=sc.nextLong(); } result= new GcdCalculation(input[0],input[1]); for(int i = 2; i < input.length; i++) { result= new GcdCalculation(result.r, input[i]); } System.out.println("Gcd of n numbers is = "+result.r); } } } |
Output:
|
1 2 3 4 5 6 |
Enter 4 numbers 4 1 2 3 Gcd of n numbers is = 1 |
